Time series methods

BSMM8740-2-R-2025F [WEEK - 6]

L.L. Odette

Recap of last week:

• Last week we introduced classification and clustering methods within the Tidymodels framework in R.
• Today we will shift gears and look at methods for analysing time series, where we use the timetk and modeltime packages in conjunction with Tidymodels to create and evaluate time series models.

This week:

• Today we will explore time series - data where each observation includes a time measurement and the time measurements are ordered.

• We’ll look at how to manipulate our time values, create time-based features, plot our time series, and decompose time series into components.

• Finally we will use our time series for forecasting, using regression, exponential smoothing and ARIMA¹ models

1. Auto Regressive Integrated Moving Average

Time Series Methods

Time series

Time series data is a data frame (tibble) with an ordered temporal measurement where measurements (error terms) may be correlated i.e. not independent.

Why can’t we use a simple linear regression model with this data? Recall that

\[ \begin{align*} \text{var}\left(\hat{\mathbf{\beta}}_{OLS}\right) & =\mathbb{E}\left[\left(\left(X'X\right)^{-1}X'\epsilon\right)\left(\left(X'X\right)^{-1}X'\epsilon\right)'\right]\\ & =\mathbb{E}\left[\left(X'X\right)^{-1}X'\epsilon\epsilon'X\left(X'X\right)^{-1}\right]\\ & =\left(X'X\right)^{-1}X'\mathbb{E}\left[\epsilon\epsilon'\right]X\left(X'X\right)^{-1} \end{align*} \]

so correlated measurements seriously compromise our fundamental OLS assumptions. And there are other way time series are unique.

Time series: characteristics

• Stationarity is a challenge with time series: Time series often exhibit trends, seasonal patterns, and structural breaks violate the assumption that the underlying data-generating process is stable over time
• Temporal ordering matters enormously in time series creating opportunities for forecasting that don’t exist in standard regression, but also requires different analytical approaches.
• The lag structure in time series creates additional complexity, where effects often occur with delays.

Time series: dynamics

Whether time series data is used for forecasting or for testing various theories/hypotheses, we try to identify the dynamic evolution of the variables. One very simple & common approach is to break the dynamics into these three parts:

\[ \begin{align*} \text{(trend)}\qquad T_{t} & =1+0.05t\qquad\\ \text{(seasonality)}\qquad S_{t} & =1.5\cos(t\pi\times0.166)\\ \text{(noise)}\qquad I_{t} & =0.5I_{t-1}+\epsilon_{t}\quad\epsilon_t\sim\mathscr{N}(0,\sigma^2) \end{align*} \]

Time series: generation

set.seed(8740)

dat <- tibble::tibble( # create a sequence of dates
  date = seq(as.Date('2015-04-7'),as.Date('2020-03-22'),'2 weeks')
) |> 
  tibble::rowid_to_column("t") |> # create time units (2 weeks)
  dplyr::mutate( # create trend and seasonality, along with noise
    trend = 1 + 0.05 * t
    , seasonality = 1.5 * cos(pi * t * 0.166)
    , noise = rnorm(length(t))
    , temp = dplyr::lag(noise)
  ) |> 
  tidyr::replace_na(list(temp = 0)) |> 
  dplyr::mutate( # modify the noise to add autocorrelation
    noise =
      purrr::map2_dbl(
        noise
        , temp
        , ~ .x + 0.5 * .y
      )
  ) |> 
  dplyr::select(-temp) # drop the temp column
dat

# A tibble: 130 × 5
       t date       trend seasonality   noise
   <int> <date>     <dbl>       <dbl>   <dbl>
 1     1 2015-04-07  1.05     1.30     1.59  
 2     2 2015-04-21  1.1      0.755    0.937 
 3     3 2015-05-05  1.15     0.00942 -0.941 
 4     4 2015-05-19  1.2     -0.739   -0.460 
 5     5 2015-06-02  1.25    -1.29     0.318 
 6     6 2015-06-16  1.3     -1.50    -0.0151
 7     7 2015-06-30  1.35    -1.31    -1.23  
 8     8 2015-07-14  1.4     -0.772   -1.55  
 9     9 2015-07-28  1.45    -0.0283   0.697 
10    10 2015-08-11  1.5      0.723   -0.0404
# ℹ 120 more rows

Time series: generation

• components
• combined

dat |> 
  tidyr::pivot_longer(-c(t, date)) |> 
  ggplot(aes(x=date, y=value, color=name)) + 
  geom_line(linewidth=1) + geom_point() + 
  labs(
    title = 'trend, seasonality, and noise'
    , subtitle = "deterministic: trend, seasonality | stochastic: noise"
    , color=NULL) + theme_minimal() + theme(plot.margin = margin(0,0,0,0, "cm"))

dat |> 
  dplyr::mutate(y = trend + seasonality + noise) |> 
  ggplot(aes(x=date, y=y)) + geom_line(linewidth=1) + geom_point(color="red") +
  labs(
    title = 'trend + seasonality + noise'
    , subtitle = "deterministic: trend, seasonality | stochastic: noise") + theme_minimal() +
  theme(plot.margin = margin(0,0,0,0, "cm"))

Time series - processes

• Time series is a collection of observations indexed by the date of each observation.

• Using notation that starts at time, \(t=1\), and using the end point, \(t=T\) the time series is a set of observations:

\[\{y_1,y_2,y_3,…,y_T\}\]

• Time index can be of any frequency (e.g. daily, quarterly, etc.).

Time series - processes

Deterministic and Stochastic Processes

• deterministic processes always produce the same output from a given starting point or state.

• stochastic processes have indeterminacy

  • Usually described by some form of statistical distribution.
  • Examples include: white noise processes, random walks, Brownian motions, Markov chains, martingale difference sequences, etc.

Time series - processes

Stochastic Processes - White noise

• A white noise series is made of serially uncorrelated random variables with zero mean and finite variance.
• For example, errors may be characterised by a Gaussian white noise process, where such a variable has a normal distribution.
• Slightly stronger condition is that they are independent from one another.

\[\epsilon_{t}\sim\text{{i.i.d.}}\mathscr{N}\left(0,\sigma_{\epsilon_{t}}^{2}\right)\]

Time series - processes

Stochastic Processes - White noise

implications:

• \(\mathbb{E}\left[\epsilon_{t}\right]=\mathbb{E}\left[\left.\epsilon_{t}\right|\epsilon_{t-1},\epsilon_{t-2},\ldots\right]=0\)
• \(\mathbb{E}\left[\epsilon_{t}\epsilon_{t-j}\right]=\text{cov}\left(\epsilon_{t},\epsilon_{t-j}\right)=0\)
• \(\text{var}\left(\epsilon_{t}\right)=\text{cov}\left(\epsilon_{t},\epsilon_{t}\right)=\sigma_{\epsilon_{t}}^{2}\)

Time series - processes

Stochastic Processes - Random walk

• Random walk definition implies that the effect of a shock is permanent. \[y_t=y_{t-1}+\epsilon_t\]
• Given the starting value \(y_0\), and using recursive substitution, this process could be represented as \[y_t=y_0+\sum_{j=1}^t\epsilon_t\]
• Since the effect of past shocks do not dissipate we say it has an infinite memory

Time series - processes

Stochastic Processes - Random walk + drift

• Random walk plus a constant term. \[y_t=\mu+y_{t-1}+\epsilon_t\]
• Given the starting value \(y_0=0\), and using recursive substitution, this process could be represented as \[y_t=\mu t+\sum_{j=1}^t\epsilon_t\]
• Shocks have permanent effects and are influenced by drift

Time series - processes

Stochastic Processes - Random walks

Characteristics:

1. Independence:
   • The steps in a random walk are independent of each other. The future position depends only on the current position and a random step.
2. Types:
   • Simple Random Walk: The step sizes are often \(\pm 1\), with equal probability.
   • General Random Walk: The step sizes can follow any distribution.
3. Applications:
   • Stock price movements, particle diffusion, and population genetics.

Time series - processes

Stochastic Processes - Markov chains

Characteristics:

1. State Space: - A Markov chain consists of a set of states and transition probabilities between these states.

2. Markov Property:

   • The probability of transitioning to the next state depends only on the current state: \(\mathbb{P}(X_{t+1} = s' | X_t = s, X_{t-1}, ..., X_0) = \mathbb{P}(X_{t+1} = s' | X_t = s)\).

3. Transition Matrix:

   • The transitions are governed by a matrix of probabilities, where each entry \(\mathsf{P}_{i,j}\) represents the probability of moving from state \(i\) to state \(j\).

4. Types:

   • Discrete-Time Markov Chain: The process is observed at discrete time intervals.
   • Continuous-Time Markov Process: The process evolves continuously over time.

5. Applications:

   • Weather modeling, queueing theory, board games (like Monopoly), speech recognition and speech generation.

Time series - processes

Stochastic Processes - Markov chains

In the discrete case, given a state transition matrix \(A\) and an initial state \(\pi_0\), then

\[ \begin{align*} \pi_1 & = \pi_0A\\ \pi_2 & = \pi_1A = \pi_0A^2\\ &\vdots\\ \pi_n & = \pi_0A^n \end{align*} \]

If the markov chain has a stationary distribution \(\pi^{s}\), then \(\pi^{s}A=\pi^{s}\) by definition and \(\pi^{s}(I-A)=0\) determines \(\pi^{s}\) up to a constant.

Time series - processes

Autoregressive Processes

• In an AR(1) process the current value is a linear function of the previous value.

\[ y_t=\phi_1 y_{t-1}+\epsilon_t \]

• Fixing the starting value at \(y_0=0\), and with repeated substitution, this process could be represented as

\[ y_t=\sum_{j=1}^t\phi_1^{t-j}\epsilon_j \]

• The distribution of each error term is \(\epsilon_t=\mathscr{N}(0,\sigma^2)\) with \(\mathbb{E}[\epsilon_i\epsilon_j]=0,\,\forall i\ne j\), and we can generalize to several lags (i.e. an AR(p) model).

Time series - processes

Moments of distribution

• The first moment of a stochastic process is the average of \(y_t\) over all possible realisations \[\hat{y}=\mathbb{E}[y_t];\;\;t=1,\ldots,T\]
• The second moment is defined as the variance \[\text{var}(y_t)=\mathbb{E}[y_t\times y_t]=\mathbb{E}[y_t- \mathbb{E}[y_t]^2];\;\;t=1,\ldots,T\]
• The covariance, for \(j\) \[\text{cov}(y_t,y_{t-j})=\mathbb{E}[y_t\times y_{t-j}]=\mathbb{E}[(y_t- \mathbb{E}[y_t])(y_{t-j}- \mathbb{E}[y_{t-j}])];\;\;t=1,\ldots,T\]

Time series - processes

Conditional moments

• Conditional distribution is based on past realisations of a random variable
• For the AR(1) model (where \(\epsilon_t\) are iid Gausian and \(|\phi|<0\)) \[y_t=\phi y_{t-1}+\epsilon_t\]
• The conditional moments are \[ \begin{align*} \mathbb{E}\left[\left.y_{t}\right|y_{t-1}\right] & =\phi y_{t-1}\\ \text{var}\left(\left.y_{t}\right|y_{t-1}\right) & =\mathbb{E}\left[\left(\phi y_{t-1}+\epsilon_{t}-\phi y_{t-1}\right)^2\right]=\mathbb{E}\left[\epsilon^2\right]=\sigma^{2}\\ \text{cov}\left(\left.y_{t}\right|y_{t-1},\left.y_{t-j}\right|y_{t-j-1}\right) & =0;\;j>1 \end{align*} \]

Time series - processes

Conditional moments

• Conditioning on \(y_{t-2}\) for \(y_t\) \[ \begin{align*} \mathbb{E}\left[\left.y_{t}\right|y_{t-2}\right] & =\phi^{2}y_{t-2}\\ \text{var}\left(\left.y_{t}\right|y_{t-2}\right) & =\left(1+\phi^{2}\right)\sigma^{2}\\ \text{cov}\left(\left.y_{t}\right|y_{t-2},\left.y_{t-j}\right|y_{t-j-2}\right) & =\phi\sigma^{2};\;j=1\\ & =0;\;j>1 \end{align*} \]

Time series - processes

Unconditional moments

• For the AR(1) model (where \(\epsilon_t\) are iid Gausian and \(|\phi|<1\)) \[y_t=\phi y_{t-1}+\epsilon_t\]
• The unconditional moments are (assuming stationarity and \(\phi<1\)) \[ \begin{align*} \mathbb{E}\left[y_{t}\right] & =0\\ \text{var}\left(y_{t}\right) & =\text{var}\left(\phi y_{t-1}+\epsilon_t\right)\\ & = \phi^2 \text{var}\left(y_{t-1}\right) + \text{var}\left(\epsilon_{t}\right)\\ & = \frac{\sigma^2}{1-\phi^2}\\ \text{cov}\left(y_{t},y_{t-k}\right) & =\phi^k\frac{\sigma^2}{1-\phi^2} \end{align*} \]

Time series - processes

Stationarity

• A time series is strictly stationary if for any \(\{j_1,j_2,\ldots,j_n\}\)
• the joint distribution of \(\{y_t,y_{t+j_1},y_{t+j_2},\ldots,y_{t+j_n}\}\)
• depends only on the intervals separating the dates \(\{j_1,j_2,\ldots,j_n\}\)
• and not on the date \(t\) itself

Time series - processes

Covariance stationary

• If neither the mean \(\hat{y}\) nor the covariance \(\text{cov}(y_t,y_{t-j})\) depend on \(t\)
• The the process for \(y_t\) is said to be covariance (weakly) stationary, where \(\forall t,j\) \[ \begin{align*} \mathbb{E}\left[y_{t}\right] & =\bar{y}\\ \mathbb{E}\left[\left(y_{t}-\bar{y}\right)\left(y_{t-j}-\bar{y}\right)\right] & =\text{cov}\left(y_{t},y_{t-j}\right) \end{align*} \]
• Note that the process \(y_t=\alpha t+\epsilon_t\) would not be stationary, as the mean clearly depends on \(t\)
• We saw that the unconditional moments of the AR(1) with \(|ϕ|<1\) had a mean and covariance that did not depend on time

Time series - processes

Autocorrelation function (ACF)

• For a stationary process we can plot the standardised covariance of the process over successive lags

• The autocovariance function is denoted by \(\gamma (j)\equiv\text{cov}(y_t,y_{t-j})\) for \(t=1,\ldots,T\)

• Tha autocovariance function is standardized by dividing each function by the variance, giving the ACF for successive values of \(j\)

  \[\rho(j)\equiv\frac{\gamma(j)}{\gamma(0)}\]

• To display the results of the ACF we usually plot \(ρ(j)\) against (non-negative) \(j\) to illustrate the degree of persistence in a variable

Time series - processes

Partial autocorrelation function (PACF)

• With an AR(1) process \(y_t=\phi y_{t-1}+\epsilon_t\), the ACF would suggest \(y_t\) and \(y_{t-2}\) are correlated, even though \(y_{t-2}\) does not appear in the model.

• This is due to the pass through, where we noted that \(y_t=\phi^2y_{t-2}\) when performing recursive substitution

• PACF eliminates the effects of passthrough and puts the focus on the independent relationship between \(y_t\) and \(y_{t_2}\)

Time series - processes

Partial autocorrelation function (PACF)

library(ggfortify)
# Parameters for the AR(1) process
phi = 0.8  # Autoregressive coefficient (should be less than 1 in absolute value)
n = 100    # Number of observations

# Simulate AR(1) process
set.seed(123)  # For reproducibility
epsilon = rnorm(n)  # White noise
X = rep(0, n)  # Initialize the series

# Generate the AR(1) series
for (t in 2:n) {
  X[t] = phi * X[t-1] + epsilon[t]
}

# Plot the AR(1) series
tibble::tibble(y=X, x=1:length(X)) |> ggplot(aes(x=x, y=y)) + geom_line() + 
  labs(title="AR(1) Process", x = "Time", y = "Value") + theme_bw(base_size = 28) + theme(plot.title = element_text(size=18)) 
# Plot the autocorrelation function (ACF)
autoplot(stats::acf(X, plot = FALSE)) + labs(title = "ACF of AR(1) Process") + theme_bw(base_size = 28) + theme(plot.title = element_text(size=18))
# Plot the autocorrelation function (ACF)
autoplot(stats::pacf(X, plot = FALSE)) + labs(title = "PACF of AR(1) Process") + theme_bw(base_size = 28) + theme(plot.title = element_text(size=18))

Time series - processes

Autoregressive Processes

• The characteristic equation for an AR(p) process is derived from the autoregressive parameters \((\phi_1, \phi_2, \ldots, \phi_p)\).

• The characteristic equation is: \(1-\phi_1 z-\phi_2 z^2-\cdots-\phi_p z^p = 0\)

• A process \({y_t}\) is strictly stationary if for each \(k\), \(t\), and \(n\), the distribution of \({y_t,\ldots,y_{t+k}}\) is the same as the distribution of \({y_{t+n},\ldots,y_{t+k+n}}\)

• For an AR process to be stationary (its statistical properties do not change over time), the parameters \(\phi_1, \phi_2, \ldots, \phi_p\) must satisfy certain conditions (typically related to the roots of the characteristic equation lying outside the unit circle¹).

1. Note: roots of polynomial may be complex numbers. The unit circle in the complex plane is the set of all complex numbers with absolute value 1.

Time series - processes

Autoregressive Processes

• An AR(p) model is sometimes expressed in terms of the Lag operator \(\mathrm{L}\), where \(\mathrm{L}y_t=y_{t-1}\). For the AR(1) process, using the lag operator we can write:

\[ \begin{align*} y_t & = \phi y_{t-1}+\epsilon_t\\ (1-\phi L)y_t & = \epsilon_t\\ y_t & = (1-\phi L)^{-1} \epsilon_t\\ & = (\sum_{i=0}^\infty\phi^i\mathrm{L}^i)\epsilon_t = \sum_{j=1}^t\phi^{t-j}\epsilon_j \end{align*} \] - EXERCISE: check that the last equality holds.

Time series - processes

Autoregressive Processes

• The lag operator can be raised to powers, e.g. \(\mathrm{L}^2y_t=y_{t-2}\) and its powers can be combined into polynomials and we can, for example, write an AR(p) process as \(\left( 1-\phi_1\mathrm{L}-\phi_2\mathrm{L}^2-\cdots -\phi_p\mathrm{L}^p\right)y_t=\epsilon_t\), or alternatively \(\Phi(L)y_t=\epsilon_t\)

Note that the roots \(\{z_1,z_2,\ldots,z_p\}\) of the characteristic equation \(1-\phi_1 z-\phi_2 z^2-\cdots-\phi_p z^p = 0\) are the same as the roots of \(\Phi(z)=(1-z/z_1)(1-z/z_2)\cdots(1-z/z_p)\) and if \(\Phi(z)^{-1}\) is to be finite, then \((1-z/z_i)^{-1}\) must be finite for every \(i\)¹

1. \((1-z/z_i)^{-1} = \sum_{i=0}^\infty(z/z_i)^i\) is finite only if \(|z/z_i|<1\)

Time series - processes

Autoregressive Processes

• Similarly \(\Phi(L)^{-1}\) exists if \((1-L/z_i)^{-1}\) is finite for every \(i\), which implies that we must have \(|L/z_i|<1, \forall i\). Since \(|L|=1\) in this context, we must have \(|z_1|>1\)

• In other words, the roots of the characteristic equation must lie outside the unit circle.

Time series - processes

Example - AR(1) process:

• The process equation is \(y_t = \phi_1 y_{t-1}+\epsilon_t\).
• The characteristic equation is \(1-\phi_1z=0\)
• the only root is \(1/\phi_1\)
• the stationarity condition is \(|1/\phi_1|>1\) or \(|\phi_1|<1\)

Time series - processes

Example - AR(2) process:

• The process equation is \(y_t = \phi_1 y_{t-1}+\phi_2 y_{t-2}+\epsilon_t\).
• The characteristic equation is \(1-\phi_1z-\phi_2 z^2=0\)
• the roots are \(\phi_1\pm\frac{\sqrt{\phi_1^2+4\phi_2}}{2\phi_2}\)
• the stationarity conditions are
  • \(|\phi_2|<1\)
  • \(\phi_2-\phi_1<1\)
  • \(\phi_1+\phi_2<1\)

Time series - processes

Unit root tests matter in business

Stationary Series:

• Predictable patterns
• Mean-reverting
• Standard econometric methods work
• Reliable forecasting

Time series - processes

Unit root tests matter in business

The Three Main Unit Root Tests

• ADF
• PP
• KPSS

The augmented Dickey–Fuller test (ADF) tests the null hypothesis that a unit root is present in a time series sample. The alternative hypothesis depends on which version of the test is used, but is usually stationarity or trend-stationarity.

tseries::adf.test(series, alternative = "stationary")

The null hypothesis of the Phillips-Perron (PP) test is that there is a unit root, with the alternative that there is no unit root. If the pvalue is above a critical size, then the null cannot be rejected.

tseries::pp.test(series, alternative = "stationary")

Kwiatkowski–Phillips–Schmidt–Shin (KPSS) tests are used for testing a null hypothesis that an observable time series is stationary around a deterministic trend (i.e. trend-stationary) against the alternative of a unit root.

Contrary to most unit root tests, the presence of a unit root is not the null hypothesis but the alternative. Additionally, in the KPSS test, the absence of a unit root is not a proof of stationarity but, by design, of trend-stationarity. This is an important distinction since it is possible for a time series to be non-stationary, have no unit root yet be trend-stationary.

tseries::kpss.test(series, null = "Trend") # or null = "Level"

Time series - processes

Unit root tests matter in business

Example

# Load the classic AirPassengers data
data(AirPassengers, package - "datasets")
log_passengers <- log(AirPassengers)

# Test for unit roots
adf_result <- tseries::adf.test(log_passengers, alternative = "stationary")
pp_result <- tseries::pp.test(log_passengers, alternative = "stationary") 
kpss_result <- tseries::kpss.test(log_passengers, null = "Trend")

# Interpretation at 5% significance level:
# ADF/PP: p < 0.05 → Reject null → Stationary
# KPSS: p < 0.05 → Reject null → Non-stationary
tibble::tibble(
  test = c("ADF Test p-value:","PP Test p-value:","KPSS Test p-value:")
  , value = c(adf_result$p.value, pp_result$p.value, kpss_result$p.value)
) |> 
  gt::gt("test") |> 
  gt::fmt_number(decimals = 4) |> 
  gt::as_raw_html()

	value
ADF Test p-value:	0.0100
PP Test p-value:	0.0100
KPSS Test p-value:	0.1000

# Plot the series
plot(log_passengers, main = "Log of Monthly Airline Passengers")

Time series - processes

Vector Autoregressive Processes

AR(p) processes can be written as AR(1) vector processes, e.g. for AR(2)

\[ \left(\begin{array}{c} y_{t}\\ y_{t-1} \end{array}\right)=\left(\begin{array}{cc} \phi_{1} & \phi_{2}\\ 1 & 0 \end{array}\right)\left(\begin{array}{c} y_{t-1}\\ y_{t-2} \end{array}\right)+\left(\begin{array}{c} \epsilon_{t}\\ 0 \end{array}\right) \] where the matrix \(A\) here is (i.e. AR(2)):

\[ A=\left(\begin{array}{cc} \phi_{1} & \phi_{2}\\ 1 & 0 \end{array}\right) \]

Time series - processes

Vector Autoregressive Processes

Repeating the argument for AR(1) processes in the vector case:

\[ \begin{align*} \vec{y}_t & = (1-A L)^{-1} \vec{\epsilon}_t\\ & = (\sum_{i=0}^\infty A^i\mathrm{L}^i)\vec{\epsilon}_t\\ \end{align*} \]

And we only converge if \(A^i\rightarrow0 \;\mathrm{as}\;i\rightarrow\infty\), i.e. all eigenvalues are < 1.

Time series - processes

Vector Autoregressive Processes

• In general if an \(n\times n\) matrix \(A\) has \(n\) distinct eigenvalues, then all eigenvalues must have magnitude \(<1\) for \(A^i\rightarrow0 \;\mathrm{as}\;i\rightarrow\infty\).
• proof: we decompose \(A=X\Lambda X^{-1}\) where the columns of \(x\) are the eigenvectors of \(A\) and \(\Lambda\) is a diagonal matrix with the eigenvalues on the diagonal.
  • so \(A^i=X\Lambda^i X^{-1}\) so \(A^i\rightarrow0 \;\mathrm{as}\;i\rightarrow\infty\)

Time series - processes

Computing determinants

1. Minor:
   • The minor \(M_{ij}\) of an element \(a_{ij}\) in an \(n \times n\) matrix \(A\) is the determinant of the \((n-1) \times (n-1)\) matrix that results from removing the \(i\)-th row and \(j\)-th column from \(A\).
2. Cofactor:
   • The cofactor \(C_{ij}\) of an element \(a_{ij}\) is given by: \(C_{ij} = (-1)^{i+j} M_{ij}\)
   • The sign factor \((-1)^{i+j}\) alternates according to the position of the element in the matrix.

Cofactor Expansion

The determinant of an \(n \times n\) matrix \(A\) can be computed by expanding along any row or column. The cofactor expansion along the \(i\)-th row is given by:

\[ \det(A) = \sum_{j=1}^n a_{ij} C_{ij} \] Similarly, the cofactor expansion along the \(j\)-th column is: \(\det(A) = \sum_{i=1}^n a_{ij} C_{ij}\)

Time series - processes

Computing determinants

The structure of the VAR(1) vector process makes it easy to compute the polynomial for the determinant in terms of the coefficients of the process.

The roots of the polynomial can be computed using polyroot, passing in a vector of polynomial coefficients in increasing order. The magnitudes of the eigenvalues can using the base function Mod.

polyroot(c(1,.2,3,.6)) |> Mod()

Time series - processes

Vector Autoregressive Processes

In a \(\text{VAR}(p)\) process we need to determine how many lags (\(p\)) to include.

• too few lags: Model misspecification, biased estimates
• too many lags: Overfitting, loss of degrees of freedom, poor forecasting

The solution is to use statistical criteria that balance model fit vs model complexity.

Time series - processes

Information Criteria

ICs balance model fit vs model complexity: in general the IC is \(\log\det(\hat{\Sigma})+\text{penalty}\times \text{parameters}/N\), where

• \(\log \det(\hat{\Sigma})\) is the log determinant of the residual covariance matrix (measures fit)
• \(\text{penalty}\) is a complexity penalty (varies by IC)
• \(N\) is the sample size

Time series - processes

Information Criteria

• Akaike Information Criterion (AIC): \(\log \det(\hat{\Sigma})+k^2p\times 2/N\)

• Hannan-Quinn Criterion (HQ): \(\log \det(\hat{\Sigma})+k^p\times 2\log(\log(N))/N\)

• Schwarz Criterion (SC/BIC): \(\log \det(\hat{\Sigma})+k^p\times \log(\log(N))/N\)

where \(k\) is the number of variables.

Time series - processes

Information Criteria

• Akaike Information Criterion (AIC)

  • tends to select more lags & good for prediction when true model is \(p=\infty\).

• Hannan-Quinn Criterion (HQ):

  penalty grows slowly.

• Schwarz Criterion (SC/BIC):

  • tends to select fewer lags & has strongest penalty for complexity.

Time series - processes

Information Criteria Example

data(Canada, package = "vars")
# Convert to regular data frame for easier handling
canada_df <- as.data.frame(Canada)
canada_df$date <- seq(as.Date("1980-01-01"), by = "quarter", length.out = nrow(Canada))

# e:    Employment (log levels)
# prod: Labor productivity (log levels)
# rw:   Real wages (log levels)
# U:    Unemployment rate (levels)
head(canada_df)

         e     prod       rw    U       date
1 929.6105 405.3665 386.1361 7.53 1980-01-01
2 929.8040 404.6398 388.1358 7.70 1980-04-01
3 930.3184 403.8149 390.5401 7.47 1980-07-01
4 931.4277 404.2158 393.9638 7.27 1980-10-01
5 932.6620 405.0467 396.7647 7.37 1981-01-01
6 933.5509 404.4167 400.0217 7.13 1981-04-01

lag_selection <- VARselect(canada_df |> dplyr::select(-date), lag.max = 8, type = "const")

# Display results
print(lag_selection$selection)

AIC(n)  HQ(n)  SC(n) FPE(n) 
     3      2      1      3 

Time series - processes

Information Criteria Example

var_dat <- canada_df |> dplyr::select(-date)
# Estimate VAR models based on different criteria
var_1 <- VAR(var_dat, p = 1, type = "const")  # SC choice
var_2 <- VAR(var_dat, p = 2, type = "const")  # HQ choice  
var_3 <- VAR(var_dat, p = 3, type = "const")  # AIC choice

• p=1
• p=2
• p=3

summary(var_1)

VAR Estimation Results:
========================= 
Endogenous variables: e, prod, rw, U 
Deterministic variables: const 
Sample size: 83 
Log Likelihood: -213.774 
Roots of the characteristic polynomial:
0.9928 0.9526 0.9526 0.7511
Call:
VAR(y = var_dat, p = 1, type = "const")


Estimation results for equation e: 
================================== 
e = e.l1 + prod.l1 + rw.l1 + U.l1 + const 

          Estimate Std. Error t value Pr(>|t|)    
e.l1       1.17354    0.08196  14.319  < 2e-16 ***
prod.l1    0.14479    0.02741   5.282 1.13e-06 ***
rw.l1     -0.07905    0.02832  -2.791  0.00660 ** 
U.l1       0.52438    0.16574   3.164  0.00222 ** 
const   -192.56361   63.81154  -3.018  0.00344 ** 
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1


Residual standard error: 0.4798 on 78 degrees of freedom
Multiple R-Squared: 0.9973, Adjusted R-squared: 0.9972 
F-statistic:  7304 on 4 and 78 DF,  p-value: < 2.2e-16 


Estimation results for equation prod: 
===================================== 
prod = e.l1 + prod.l1 + rw.l1 + U.l1 + const 

         Estimate Std. Error t value Pr(>|t|)    
e.l1      0.08710    0.11823   0.737    0.464    
prod.l1   1.01970    0.03955  25.785   <2e-16 ***
rw.l1    -0.02629    0.04085  -0.644    0.522    
U.l1      0.32299    0.23910   1.351    0.181    
const   -81.55110   92.05141  -0.886    0.378    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1


Residual standard error: 0.6921 on 78 degrees of freedom
Multiple R-Squared: 0.9746, Adjusted R-squared: 0.9733 
F-statistic: 747.4 on 4 and 78 DF,  p-value: < 2.2e-16 


Estimation results for equation rw: 
=================================== 
rw = e.l1 + prod.l1 + rw.l1 + U.l1 + const 

         Estimate Std. Error t value Pr(>|t|)    
e.l1      0.06381    0.13481   0.473  0.63729    
prod.l1  -0.13551    0.04509  -3.005  0.00357 ** 
rw.l1     0.96873    0.04658  20.797  < 2e-16 ***
U.l1     -0.19538    0.27262  -0.717  0.47571    
const    11.61376  104.96033   0.111  0.91218    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1


Residual standard error: 0.7892 on 78 degrees of freedom
Multiple R-Squared: 0.9988, Adjusted R-squared: 0.9988 
F-statistic: 1.681e+04 on 4 and 78 DF,  p-value: < 2.2e-16 


Estimation results for equation U: 
================================== 
U = e.l1 + prod.l1 + rw.l1 + U.l1 + const 

         Estimate Std. Error t value Pr(>|t|)    
e.l1     -0.19294    0.06129  -3.148 0.002331 ** 
prod.l1  -0.08087    0.02050  -3.944 0.000174 ***
rw.l1     0.07539    0.02118   3.559 0.000637 ***
U.l1      0.47531    0.12396   3.835 0.000254 ***
const   186.80892   47.72282   3.914 0.000193 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1


Residual standard error: 0.3588 on 78 degrees of freedom
Multiple R-Squared: 0.9524, Adjusted R-squared:  0.95 
F-statistic: 390.5 on 4 and 78 DF,  p-value: < 2.2e-16 



Covariance matrix of residuals:
            e     prod       rw        U
e     0.23020  0.05311 -0.10293 -0.14055
prod  0.05311  0.47903  0.02617 -0.02913
rw   -0.10293  0.02617  0.62281  0.08092
U    -0.14055 -0.02913  0.08092  0.12875

Correlation matrix of residuals:
           e    prod      rw       U
e     1.0000  0.1599 -0.2718 -0.8164
prod  0.1599  1.0000  0.0479 -0.1173
rw   -0.2718  0.0479  1.0000  0.2857
U    -0.8164 -0.1173  0.2857  1.0000

summary(var_2)

VAR Estimation Results:
========================= 
Endogenous variables: e, prod, rw, U 
Deterministic variables: const 
Sample size: 82 
Log Likelihood: -175.819 
Roots of the characteristic polynomial:
0.995 0.9081 0.9081 0.7381 0.7381 0.1856 0.1429 0.1429
Call:
VAR(y = var_dat, p = 2, type = "const")


Estimation results for equation e: 
================================== 
e = e.l1 + prod.l1 + rw.l1 + U.l1 + e.l2 + prod.l2 + rw.l2 + U.l2 + const 

          Estimate Std. Error t value Pr(>|t|)    
e.l1     1.638e+00  1.500e-01  10.918  < 2e-16 ***
prod.l1  1.673e-01  6.114e-02   2.736  0.00780 ** 
rw.l1   -6.312e-02  5.524e-02  -1.143  0.25692    
U.l1     2.656e-01  2.028e-01   1.310  0.19444    
e.l2    -4.971e-01  1.595e-01  -3.116  0.00262 ** 
prod.l2 -1.017e-01  6.607e-02  -1.539  0.12824    
rw.l2    3.844e-03  5.552e-02   0.069  0.94499    
U.l2     1.327e-01  2.073e-01   0.640  0.52418    
const   -1.370e+02  5.585e+01  -2.453  0.01655 *  
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1


Residual standard error: 0.3628 on 73 degrees of freedom
Multiple R-Squared: 0.9985, Adjusted R-squared: 0.9984 
F-statistic:  6189 on 8 and 73 DF,  p-value: < 2.2e-16 


Estimation results for equation prod: 
===================================== 
prod = e.l1 + prod.l1 + rw.l1 + U.l1 + e.l2 + prod.l2 + rw.l2 + U.l2 + const 

          Estimate Std. Error t value Pr(>|t|)    
e.l1      -0.17277    0.26977  -0.640  0.52390    
prod.l1    1.15043    0.10995  10.464 3.57e-16 ***
rw.l1      0.05130    0.09934   0.516  0.60710    
U.l1      -0.47850    0.36470  -1.312  0.19362    
e.l2       0.38526    0.28688   1.343  0.18346    
prod.l2   -0.17241    0.11881  -1.451  0.15104    
rw.l2     -0.11885    0.09985  -1.190  0.23778    
U.l2       1.01592    0.37285   2.725  0.00805 ** 
const   -166.77552  100.43388  -1.661  0.10109    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1


Residual standard error: 0.6525 on 73 degrees of freedom
Multiple R-Squared: 0.9787, Adjusted R-squared: 0.9764 
F-statistic: 419.3 on 8 and 73 DF,  p-value: < 2.2e-16 


Estimation results for equation rw: 
=================================== 
rw = e.l1 + prod.l1 + rw.l1 + U.l1 + e.l2 + prod.l2 + rw.l2 + U.l2 + const 

          Estimate Std. Error t value Pr(>|t|)    
e.l1     -0.268833   0.322619  -0.833    0.407    
prod.l1  -0.081065   0.131487  -0.617    0.539    
rw.l1     0.895478   0.118800   7.538 1.04e-10 ***
U.l1      0.012130   0.436149   0.028    0.978    
e.l2      0.367849   0.343087   1.072    0.287    
prod.l2  -0.005181   0.142093  -0.036    0.971    
rw.l2     0.052677   0.119410   0.441    0.660    
U.l2     -0.127708   0.445892  -0.286    0.775    
const   -33.188339 120.110525  -0.276    0.783    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1


Residual standard error: 0.7803 on 73 degrees of freedom
Multiple R-Squared: 0.9989, Adjusted R-squared: 0.9987 
F-statistic:  8009 on 8 and 73 DF,  p-value: < 2.2e-16 


Estimation results for equation U: 
================================== 
U = e.l1 + prod.l1 + rw.l1 + U.l1 + e.l2 + prod.l2 + rw.l2 + U.l2 + const 

         Estimate Std. Error t value Pr(>|t|)    
e.l1     -0.58076    0.11563  -5.023 3.49e-06 ***
prod.l1  -0.07812    0.04713  -1.658 0.101682    
rw.l1     0.01866    0.04258   0.438 0.662463    
U.l1      0.61893    0.15632   3.959 0.000173 ***
e.l2      0.40982    0.12296   3.333 0.001352 ** 
prod.l2   0.05212    0.05093   1.023 0.309513    
rw.l2     0.04180    0.04280   0.977 0.331928    
U.l2     -0.07117    0.15981  -0.445 0.657395    
const   149.78056   43.04810   3.479 0.000851 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1


Residual standard error: 0.2797 on 73 degrees of freedom
Multiple R-Squared: 0.9726, Adjusted R-squared: 0.9696 
F-statistic:   324 on 8 and 73 DF,  p-value: < 2.2e-16 



Covariance matrix of residuals:
             e      prod       rw        U
e     0.131635 -0.007469 -0.04210 -0.06909
prod -0.007469  0.425711  0.06461  0.01392
rw   -0.042099  0.064613  0.60886  0.03422
U    -0.069087  0.013923  0.03422  0.07821

Correlation matrix of residuals:
            e     prod      rw       U
e     1.00000 -0.03155 -0.1487 -0.6809
prod -0.03155  1.00000  0.1269  0.0763
rw   -0.14870  0.12691  1.0000  0.1568
U    -0.68090  0.07630  0.1568  1.0000

summary(var_3)

VAR Estimation Results:
========================= 
Endogenous variables: e, prod, rw, U 
Deterministic variables: const 
Sample size: 81 
Log Likelihood: -150.609 
Roots of the characteristic polynomial:
1.004 0.9283 0.9283 0.7437 0.7437 0.6043 0.6043 0.5355 0.5355 0.2258 0.2258 0.1607
Call:
VAR(y = var_dat, p = 3, type = "const")


Estimation results for equation e: 
================================== 
e = e.l1 + prod.l1 + rw.l1 + U.l1 + e.l2 + prod.l2 + rw.l2 + U.l2 + e.l3 + prod.l3 + rw.l3 + U.l3 + const 

          Estimate Std. Error t value Pr(>|t|)    
e.l1       1.75274    0.15082  11.622  < 2e-16 ***
prod.l1    0.16962    0.06228   2.723 0.008204 ** 
rw.l1     -0.08260    0.05277  -1.565 0.122180    
U.l1       0.09952    0.19747   0.504 0.615915    
e.l2      -1.18385    0.23517  -5.034 3.75e-06 ***
prod.l2   -0.10574    0.09425  -1.122 0.265858    
rw.l2     -0.02439    0.06957  -0.351 0.727032    
U.l2      -0.05077    0.24534  -0.207 0.836667    
e.l3       0.58725    0.16431   3.574 0.000652 ***
prod.l3    0.01054    0.06384   0.165 0.869371    
rw.l3      0.03824    0.05365   0.713 0.478450    
U.l3       0.34139    0.20530   1.663 0.100938    
const   -150.68737   61.00889  -2.470 0.016029 *  
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1


Residual standard error: 0.3399 on 68 degrees of freedom
Multiple R-Squared: 0.9988, Adjusted R-squared: 0.9985 
F-statistic:  4554 on 12 and 68 DF,  p-value: < 2.2e-16 


Estimation results for equation prod: 
===================================== 
prod = e.l1 + prod.l1 + rw.l1 + U.l1 + e.l2 + prod.l2 + rw.l2 + U.l2 + e.l3 + prod.l3 + rw.l3 + U.l3 + const 

          Estimate Std. Error t value Pr(>|t|)    
e.l1      -0.14880    0.28913  -0.515   0.6085    
prod.l1    1.14799    0.11940   9.615 2.65e-14 ***
rw.l1      0.02359    0.10117   0.233   0.8163    
U.l1      -0.65814    0.37857  -1.739   0.0866 .  
e.l2      -0.18165    0.45083  -0.403   0.6883    
prod.l2   -0.19627    0.18069  -1.086   0.2812    
rw.l2     -0.20337    0.13337  -1.525   0.1319    
U.l2       0.82237    0.47034   1.748   0.0849 .  
e.l3       0.57495    0.31499   1.825   0.0723 .  
prod.l3    0.04415    0.12239   0.361   0.7194    
rw.l3      0.09337    0.10285   0.908   0.3672    
U.l3       0.40078    0.39357   1.018   0.3121    
const   -195.86985  116.95813  -1.675   0.0986 .  
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1


Residual standard error: 0.6515 on 68 degrees of freedom
Multiple R-Squared:  0.98,  Adjusted R-squared: 0.9765 
F-statistic: 277.5 on 12 and 68 DF,  p-value: < 2.2e-16 


Estimation results for equation rw: 
=================================== 
rw = e.l1 + prod.l1 + rw.l1 + U.l1 + e.l2 + prod.l2 + rw.l2 + U.l2 + e.l3 + prod.l3 + rw.l3 + U.l3 + const 

          Estimate Std. Error t value Pr(>|t|)    
e.l1    -4.716e-01  3.373e-01  -1.398    0.167    
prod.l1 -6.500e-02  1.393e-01  -0.467    0.642    
rw.l1    9.091e-01  1.180e-01   7.702 7.63e-11 ***
U.l1    -7.941e-04  4.417e-01  -0.002    0.999    
e.l2     6.667e-01  5.260e-01   1.268    0.209    
prod.l2 -2.164e-01  2.108e-01  -1.027    0.308    
rw.l2   -1.457e-01  1.556e-01  -0.936    0.353    
U.l2    -3.014e-01  5.487e-01  -0.549    0.585    
e.l3    -1.289e-01  3.675e-01  -0.351    0.727    
prod.l3  2.140e-01  1.428e-01   1.498    0.139    
rw.l3    1.902e-01  1.200e-01   1.585    0.118    
U.l3     1.506e-01  4.592e-01   0.328    0.744    
const   -1.167e+01  1.365e+02  -0.086    0.932    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1


Residual standard error: 0.7601 on 68 degrees of freedom
Multiple R-Squared: 0.9989, Adjusted R-squared: 0.9987 
F-statistic:  5239 on 12 and 68 DF,  p-value: < 2.2e-16 


Estimation results for equation U: 
================================== 
U = e.l1 + prod.l1 + rw.l1 + U.l1 + e.l2 + prod.l2 + rw.l2 + U.l2 + e.l3 + prod.l3 + rw.l3 + U.l3 + const 

         Estimate Std. Error t value Pr(>|t|)    
e.l1     -0.61773    0.12508  -4.939 5.39e-06 ***
prod.l1  -0.09778    0.05165  -1.893 0.062614 .  
rw.l1     0.01455    0.04377   0.332 0.740601    
U.l1      0.65976    0.16378   4.028 0.000144 ***
e.l2      0.51811    0.19504   2.656 0.009830 ** 
prod.l2   0.08799    0.07817   1.126 0.264279    
rw.l2     0.06993    0.05770   1.212 0.229700    
U.l2     -0.08099    0.20348  -0.398 0.691865    
e.l3     -0.03006    0.13627  -0.221 0.826069    
prod.l3  -0.01092    0.05295  -0.206 0.837180    
rw.l3    -0.03909    0.04450  -0.879 0.382733    
U.l3      0.06684    0.17027   0.393 0.695858    
const   114.36732   50.59802   2.260 0.027008 *  
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1


Residual standard error: 0.2819 on 68 degrees of freedom
Multiple R-Squared: 0.9736, Adjusted R-squared: 0.969 
F-statistic: 209.2 on 12 and 68 DF,  p-value: < 2.2e-16 



Covariance matrix of residuals:
            e     prod       rw        U
e     0.11550 -0.03161 -0.03681 -0.07034
prod -0.03161  0.42449  0.05589  0.01494
rw   -0.03681  0.05589  0.57780  0.03660
U    -0.07034  0.01494  0.03660  0.07945

Correlation matrix of residuals:
           e     prod      rw        U
e     1.0000 -0.14276 -0.1425 -0.73426
prod -0.1428  1.00000  0.1129  0.08136
rw   -0.1425  0.11286  1.0000  0.17084
U    -0.7343  0.08136  0.1708  1.00000

Time series - processes

Moving Average Processes

• In an MA(q) process the present value is a weighted sum on the current and previous errors. \[y_t= \epsilon_t +\theta_1\epsilon_{t-1};\;\text(MA(1))\]
• MA(q) models describe processes where it takes a bit of time for the error (or “shock”) to dissipate
• This type of expression may be used to describe a wide variety of stationary time series processes

Time series - processes

Moving Average Processes

• There is a duality of AR() and MA() processes.

• We have already seen how AR processes can be expressed as MA() processes:

\[ \vec{y}_t = (1-A L)^{-1} \vec{\epsilon}_t = (\sum_{i=0}^\infty A^i\mathrm{L}^i)\vec{\epsilon}_t\\ \]

and MA() processes can be expressed as AR processes by a similar argument.

Time series - processes

ARMA Processes

• A combination of an AR(1) and a MA(1) process is termed an ARMA(1,1) observation. \[y_t=\phi y_{t-1}+\epsilon_t+\theta\epsilon_{t-1}\]
• An ARMA(p,q) process takes the form \[y_t=\sum_{j=1}^p\phi_jy_{t-j}+\epsilon_t+\sum_{i=1}^q\theta_i\epsilon_{t-i}\]
• This model was popularized by Box & Jenkins, who developed a methodology that may be used to identify the terms that should be included in the model

Time series - processes

Long memory & fractional differencing

• Most AR(p), MA(q) and ARMA(p,q) processes are termed short-memory process because the coefficients in the representation are dominated by exponential decay
• Long-memory (or persistent) time series are considered intermediate compromises between the short-memory models and integrated nonstationary processes

Time series - processes

ARIMA

• AutoRegressive Integrated Moving Average combines three key concepts: autoregression (AR), differencing (I - for Integrated), and moving average (MA).
• AR (AutoRegressive): captures the relationship between an observation and lagged observations.
• I (Integrated): Differencing is used to make the time series stationary.
• MA (Moving Average): captures the relationship between an observation and a residual error from a moving average model.
• An ARIMA model is denoted as ARIMA(p, d, q), where: - p is the number of lag observations in the model (AR part), - d is the number of times that the raw observations are differenced (I part), - q is the size of the moving average window (MA part).

Time series - processes

ARIMA

The ARIMA time series modeling package we will be using has an auto-ARIMA function which can suggest the \(p\),\(d\), and \(q\) values that give the best fit to the data, along with computing the corresponding parameter estimates.

Time series - exponential smoothing

Exponential smoothing or exponential moving average (EMA) is a technique for smoothing time series data using the exponential window function.

For a raw data series \(\{x_t\}\) the output of the exponential smoothing process is \(\{y_t\}\), where, for \(0\le\alpha\le1\) and \(t>0\)

\[ \begin{align*} y_0 & = x_0 \\ y_t & = \alpha x_t + (1-\alpha)y_{t-1} \end{align*} \]

\(\alpha\) is called the smoothing factor.

Time series - exponential smoothing

Continuing on:

\[ \begin{align*} y_{t} & =\alpha x_{t}+\alpha(1-\alpha)x_{t-1}+(1-\alpha)^{2}y_{t-2}\\ y_{t} & =\alpha x_{t}+\alpha(1-\alpha)x_{t-1}+\alpha(1-\alpha)^{2}x_{t-2}+(1-\alpha)^{3}y_{t-3}\\ y_{t} & =\alpha\sum_{i=0}^{\infty}(1-\alpha)^{i}x_{t-i} \end{align*} \] The time constant \(\tau\) is the number of time periods needed for the weight on past \(x\) to reach \(e^{-1}\) or 36.7%.

Time series - exponential smoothing

To find \(\tau\) in the discrete-time case we solve

\[ (1-\alpha)^{k}=e^{-\frac{k}{\tau}}\rightarrow\tau=\frac{-1}{\log(1-\alpha)}=\frac{1}{\alpha+\alpha^2/2+\alpha^3/3+\ldots} \] so for small \(\alpha\), \(\tau\approx 1/\alpha\).

The time constant \(\tau\) provides an intuitive measure of:

1. Response speed: How quickly the model adapts to changes

2. Memory span: How far back the model effectively looks

3. Smoothing intensity: How much noise reduction occurs

Time series - exponential smoothing

We can also include a trend term

\[ \begin{align*} y_0 & = x_0 \\ b_0 & = x_1 - x_0\\ \end{align*} \]

and for \(t>0\), \(0\le\alpha\le1\) and \(0\le\beta\le1\)

\[ \begin{align*} y_t & = \alpha x_t + (1-\alpha)(y_{t-1} + b_{t-1})\\ b_t & = \beta(y_t-y_{t-1}) + (1-\beta)b_{t-1} \end{align*} \]

Time series - exponential smoothing

Finally we can also include a seasonality term¹, with a cycle length of \(L\) time intervals.

and for \(t>0\), \(0\le\alpha\le1\), \(0\le\beta\le1\) and \(0\le\gamma\le1-\alpha\)

\[ \begin{align*} y_t & = \alpha \frac{x_t}{c_{t-L}} + (1-\alpha)(y_{t-1} + b_{t-1})\\ b_t & = \beta(y_t-y_{t-1}) + (1-\beta)b_{t-1}\\ c_t & = \gamma\frac{x_t}{y_t} + (1-\gamma)c_{t-L} \end{align*} \]

1. note that this seasonality is multiplicative

Time series - ETS models

ETS stands for Error-Trend-Seasonality, and the exponential smoothing model is clearly in this class, with each component additive. The more general taxonomy is:

• Error: “Additive” (A), or “Multiplicative” (M);
• Trend: “None” (N), “Additive” (A), “Additive damped” (Ad), “Multiplicative” (M), or “Multiplicative damped” (Md);
• Seasonality: “None” (N), or “Additive” (A), or “Multiplicative” (M).

In this taxonomy, the exponential smoothing model is denoted as ETS(A,A,M).

Time series - ETS models

The additive ETS models are shown below, and more detailed discussion can be found here

Time series - ETS models

In modeltime these models, including seasonal decomposition models, are specified using modeltime::seasonal_reg(), for regression models only, with the following engines

• parsnip::set_engine("stlm_ets") for auto-ETS

• parsnip::set_engine("stlm_arima") for auto-arima

• parsnip::set_engine("tbats") for TBATS models: Trigonometric seasonality, Box-Cox transformation, ARMA errors, Trend and Seasonal components.

Only stlm_arima accepts covariates.

Time series - ETS models

It is often useful to have a baseline model to compare all other models to.

In modeltime we often use the NAIVE or SNAIVE (seasonal naive) models, where a naive forecast predicts the future value a the most recent observed value.

These models are specified with modeltime::naive_reg(), with a seasonal_period argument in the specification for use if the seasonal period is known - otherwise the default is ‘auto.’

The corresponding engine is parsnip::set_engine('naive').

The Timetk package

Time series - plotting

timetk::bike_sharing_daily |> 
  dplyr::slice_head(n=5) |> 
  dplyr::glimpse()

Rows: 5
Columns: 16
$ instant    <dbl> 1, 2, 3, 4, 5
$ dteday     <date> 2011-01-01, 2011-01-02, 2011-01-03, 2011-01-04, 2011-01-05
$ season     <dbl> 1, 1, 1, 1, 1
$ yr         <dbl> 0, 0, 0, 0, 0
$ mnth       <dbl> 1, 1, 1, 1, 1
$ holiday    <dbl> 0, 0, 0, 0, 0
$ weekday    <dbl> 6, 0, 1, 2, 3
$ workingday <dbl> 0, 0, 1, 1, 1
$ weathersit <dbl> 2, 2, 1, 1, 1
$ temp       <dbl> 0.344167, 0.363478, 0.196364, 0.200000, 0.226957
$ atemp      <dbl> 0.363625, 0.353739, 0.189405, 0.212122, 0.229270
$ hum        <dbl> 0.805833, 0.696087, 0.437273, 0.590435, 0.436957
$ windspeed  <dbl> 0.160446, 0.248539, 0.248309, 0.160296, 0.186900
$ casual     <dbl> 331, 131, 120, 108, 82
$ registered <dbl> 654, 670, 1229, 1454, 1518
$ cnt        <dbl> 985, 801, 1349, 1562, 1600

Time series - plotting

The timetk::plot_time_series() function is a good way to to get a quick timeseries plot. From a tidy table we

• select the time value and the columns we want to plot
• pivot (longer) the columns we want to plot
• plot

The timetk::plot_time_series() function has many options that can be used to customize the plot.

Time series - plotting

timetk::bike_sharing_daily |> 
  dplyr::select(dteday, casual, registered) |> 
  tidyr::pivot_longer(-dteday) |> 
  timetk::plot_time_series(
    .date_var = dteday
    , .value = value
    , .color_var = name
  )

Time series - timetk::

time downscaling

timetk::bike_sharing_daily |> 
  timetk::summarise_by_time(
    .date_var = dteday
    , .by = "week"
    , .week_start = 7
    , causal = sum(casual)
    , registered = mean(registered)
    , max_cnt = max(cnt)
  )

# A tibble: 106 × 4
   dteday     causal registered max_cnt
   <date>      <dbl>      <dbl>   <dbl>
 1 2010-12-26    331       654      985
 2 2011-01-02    745      1235.    1606
 3 2011-01-09    477      1167.    1421
 4 2011-01-16    706      1183.    1927
 5 2011-01-23    632       994.    1985
 6 2011-01-30    550      1314.    1708
 7 2011-02-06   1075      1450.    1746
 8 2011-02-13   2333      1734.    2927
 9 2011-02-20   1691      1405.    1969
10 2011-02-27   2120      1631.    2402
# ℹ 96 more rows

Time series - timetk::

time upscaling

timetk::bike_sharing_daily |> 
  dplyr::select(dteday, casual) |> 
  timetk::pad_by_time(.date_var = dteday, .by = "hour") |> 
  timetk::mutate_by_time(
    .date_var = dteday
    , .by = "day"
    , casual = sum(casual,na.rm=T)/24
  )

# A tibble: 17,521 × 2
   dteday              casual
   <dttm>               <dbl>
 1 2011-01-01 00:00:00   13.8
 2 2011-01-01 01:00:00   13.8
 3 2011-01-01 02:00:00   13.8
 4 2011-01-01 03:00:00   13.8
 5 2011-01-01 04:00:00   13.8
 6 2011-01-01 05:00:00   13.8
 7 2011-01-01 06:00:00   13.8
 8 2011-01-01 07:00:00   13.8
 9 2011-01-01 08:00:00   13.8
10 2011-01-01 09:00:00   13.8
# ℹ 17,511 more rows

Time series - timetk::

time filtering

timetk::bike_sharing_daily |>
  timetk::filter_by_time(
    .date_var = dteday
    , .start_date="2012-01-15"
    , .end_date = "2012-07-01"
  ) |> 
  timetk::plot_time_series(.date_var = dteday, casual)

Time series - timetk::

time offsets

require(timetk, quietly = FALSE)
timetk::bike_sharing_daily |>
  timetk::filter_by_time(
    .date_var = dteday
    , .start_date="2012-01-15"
    , .end_date = "2012-01-15" %+time% "12 weeks"
  ) |> 
  timetk::plot_time_series(.date_var = dteday, casual)

Time series - timetk::

mutate by period

timetk::bike_sharing_daily |>
  dplyr::select(dteday, casual) |> 
  timetk::mutate_by_time(
    .date_var = dteday
    , .by = "7 days"
    , casual_mean = mean(casual)
    , casual_median = median(casual)
    , casual_max = max(casual)
    , casual_min = min(casual)
  )

# A tibble: 731 × 6
   dteday     casual casual_mean casual_median casual_max casual_min
   <date>      <dbl>       <dbl>         <dbl>      <dbl>      <dbl>
 1 2011-01-01    331       144             120        331         82
 2 2011-01-02    131       144             120        331         82
 3 2011-01-03    120       144             120        331         82
 4 2011-01-04    108       144             120        331         82
 5 2011-01-05     82       144             120        331         82
 6 2011-01-06     88       144             120        331         82
 7 2011-01-07    148       144             120        331         82
 8 2011-01-08     68        46.1            43         68         25
 9 2011-01-09     54        46.1            43         68         25
10 2011-01-10     41        46.1            43         68         25
# ℹ 721 more rows

Time series - timetk::

summarize by period

timetk::bike_sharing_daily |>
  timetk::summarize_by_time(
    .date_var = dteday
    , .by = "7 days"
    , casual_mean = mean(casual)
    , registered_mean = mean(registered)
    , windspeed_max = max(windspeed)
  )

# A tibble: 119 × 4
   dteday     casual_mean registered_mean windspeed_max
   <date>           <dbl>           <dbl>         <dbl>
 1 2011-01-01       144             1201.         0.249
 2 2011-01-08        46.1           1147.         0.362
 3 2011-01-15       119.            1203.         0.353
 4 2011-01-22        86              981.         0.294
 5 2011-01-29       102.            1130          0.187
 6 2011-02-01       120.            1377.         0.278
 7 2011-02-08       172.            1455.         0.418
 8 2011-02-15       366             1618.         0.507
 9 2011-02-22       233.            1546.         0.347
10 2011-03-01       243.            1495          0.343
# ℹ 109 more rows

Time series - timetk::

create a timeseries

tibble::tibble(
  date = 
    timetk::tk_make_timeseries(
      start_date = "2025"
      , length_out = 100
      , by = "month"
    )
  , values=1:100
)

# A tibble: 100 × 2
   date       values
   <date>      <int>
 1 2025-01-01      1
 2 2025-02-01      2
 3 2025-03-01      3
 4 2025-04-01      4
 5 2025-05-01      5
 6 2025-06-01      6
 7 2025-07-01      7
 8 2025-08-01      8
 9 2025-09-01      9
10 2025-10-01     10
# ℹ 90 more rows

Time series - timetk::

create a timeseries

timetk::tk_make_holiday_sequence(
  start_date = "2025"
  , end_date = "2027"
  , calendar = "TSX"
) %>% 
  timetk::tk_get_holiday_signature(holiday_pattern = "Thanksgiving",locale_set = "CA", exchange = "TSX") |> 
  dplyr::slice_head(n = 6) |> 
  dplyr::glimpse()

Rows: 6
Columns: 6
$ index              <date> 2025-01-01, 2025-02-17, 2025-02-17, 2025-02-17, 20…
$ exch_TSX           <dbl> 1, 1, 1, 1, 1, 1
$ locale_CA          <dbl> 0, 1, 1, 1, 0, 1
$ CA_ThanksgivingDay <dbl> 0, 0, 0, 0, 0, 0
$ JP_ThanksgivingDay <dbl> 0, 0, 0, 0, 0, 0
$ US_ThanksgivingDay <dbl> 0, 0, 0, 0, 0, 0

Time series - timetk::

• raw
• box-cox transformed

# plot wind speed
timetk::bike_sharing_daily |> 
  timetk::plot_time_series(dteday, windspeed, .title = "Time Series - Raw")

# plot transformed speed
timetk::bike_sharing_daily |> 
  timetk::plot_time_series(
    dteday
    , timetk::box_cox_vec(windspeed, lambda="auto",  silent = T)
    , .title = "Time Series - Box Cox Tranformed")

Time series - timetk::

timeseries transformations

See Also

• Lag Transformation: lag_vec()

• Differencing Transformation: diff_vec()

• Rolling Window Transformation: slidify_vec()

• Loess Smoothing Transformation: smooth_vec()

• Fourier Series: fourier_vec()

• Missing Value Imputation for Time Series: ts_impute_vec(), ts_clean_vec()

Other common transformations to reduce variance: log(), log1p() and sqrt()

Time series - Feature engineering

• feature engineering
• plot

subscribers_tbl   <- readRDS("data/00_data/mailchimp_users.rds")

data_prepared_tbl <- subscribers_tbl |> 
  timetk::summarize_by_time(optin_time, .by="day", optins=dplyr::n()) |> 
  timetk::pad_by_time(.pad_value=0) |> 
  # preprocessing
  dplyr::mutate(optins_trans=timetk::log_interval_vec(optins, limit_lower=0, offset=1)) |> 
  dplyr::mutate(optins_trans=timetk::standardize_vec(optins_trans)) |> 
  # fix missing vals at start
  timetk::filter_by_time(.start_date = "2018-07-03") |> 
  # outliers clean
  dplyr::mutate(optins_trans_cleaned = timetk::ts_clean_vec(optins_trans, period=7)) |> 
  dplyr::mutate(optins_trans=ifelse(optin_time |> timetk::between_time("2018-11-18","2018-11-20")
                             , optins_trans_cleaned
                             , optins_trans
                             )) |> 
  dplyr::select(-optins, -optins_trans_cleaned)
# show the dt  
data_prepared_tbl     

# A tibble: 609 × 2
   optin_time optins_trans
   <date>            <dbl>
 1 2018-07-03      -0.492 
 2 2018-07-04      -0.153 
 3 2018-07-05      -0.578 
 4 2018-07-06      -0.413 
 5 2018-07-07      -1.20  
 6 2018-07-08      -1.66  
 7 2018-07-09      -0.274 
 8 2018-07-10      -0.212 
 9 2018-07-11      -0.0986
10 2018-07-12      -0.274 
# ℹ 599 more rows

data_prepared_tbl |> # plot the table
  tidyr::pivot_longer(contains("trans")) |> 
  timetk::plot_time_series(optin_time,value,name) 

Date Features

data_prep_signature_tbl <- 
  data_prepared_tbl |> 
  timetk::tk_augment_timeseries_signature(
    .date_var = optin_time
  ) 

Rows: 4
Columns: 30
$ optin_time   <date> 2018-07-03, 2018-07-04, 2018-07-05, 2018-07-06
$ optins_trans <dbl> -0.4919060, -0.1534053, -0.5779424, -0.4133393
$ index.num    <dbl> 1530576000, 1530662400, 1530748800, 1530835200
$ diff         <dbl> NA, 86400, 86400, 86400
$ year         <int> 2018, 2018, 2018, 2018
$ year.iso     <int> 2018, 2018, 2018, 2018
$ half         <int> 2, 2, 2, 2
$ quarter      <int> 3, 3, 3, 3
$ month        <int> 7, 7, 7, 7
$ month.xts    <int> 6, 6, 6, 6
$ month.lbl    <ord> July, July, July, July
$ day          <int> 3, 4, 5, 6
$ hour         <int> 0, 0, 0, 0
$ minute       <int> 0, 0, 0, 0
$ second       <int> 0, 0, 0, 0
$ hour12       <int> 0, 0, 0, 0
$ am.pm        <int> 1, 1, 1, 1
$ wday         <int> 3, 4, 5, 6
$ wday.xts     <int> 2, 3, 4, 5
$ wday.lbl     <ord> Tuesday, Wednesday, Thursday, Friday
$ mday         <int> 3, 4, 5, 6
$ qday         <int> 3, 4, 5, 6
$ yday         <int> 184, 185, 186, 187
$ mweek        <int> 1, 1, 1, 1
$ week         <int> 27, 27, 27, 27
$ week.iso     <int> 27, 27, 27, 27
$ week2        <int> 1, 1, 1, 1
$ week3        <int> 0, 0, 0, 0
$ week4        <int> 3, 3, 3, 3
$ mday7        <int> 1, 1, 1, 1

Trend

data_prep_signature_tbl |> 
  timetk::plot_time_series_regression(
    .date_var = optin_time
    , .formula = optins_trans ~ index.num
  )

Non-linear trends

• B-spline, degree 3
• Cubic spline, 3 knots

data_prep_signature_tbl |> 
  timetk::plot_time_series_regression(
    .date_var = optin_time
    , .formula = optins_trans ~ splines::bs(index.num, degree=3)
    , .show_summary = FALSE
    , .title = "B-spline, degree 3"
  )

data_prep_signature_tbl |> 
  timetk::plot_time_series_regression(
    .date_var=optin_time
    , .formula=
      optins_trans ~ splines::ns(
        index.num
        , knots=quantile(index.num, probs=c(0.25, 0.5, 0.75)))
    , .show_summary = FALSE
    , .title = "Cubic spline, 3 knots"
  )

Seasonality

• weekly
• monthly

# Weekly Seasonality
data_prep_signature_tbl |> 
  timetk::plot_time_series_regression(
    .date_var=optin_time
    , .formula=optins_trans ~ wday.lbl + splines::bs(index.num, degree=3)
    , .show_summary = FALSE
    , .title = "Weekday seasonality"
  )

data_prep_signature_tbl |> 
  timetk::plot_time_series_regression(
    .date_var=optin_time
    , .formula=optins_trans ~ month.lbl + splines::bs(index.num, degree=3)
    , .show_summary = FALSE
    , .title = "Monthly seasonality"
  )

Seasonality

# ** Together with Trend
model_formula_seasonality <- as.formula(
  optins_trans ~ wday.lbl + month.lbl +
    splines::ns(index.num
                , knots=quantile(index.num, probs=c(0.25, 0.5, 0.75))) + .
)
data_prep_signature_tbl |> 
  timetk::plot_time_series_regression(
    .date_var=optin_time
    , .formula = model_formula_seasonality
    , .show_summary = FALSE
    , .title = "Day and Month seasonality + Cubic spline, 3 knots"
  )

Fourier series

data_prep_signature_tbl |> 
  timetk::plot_acf_diagnostics(optin_time,optins_trans)

Fourier series

data_prep_fourier_tbl <- 
  data_prep_signature_tbl |> 
  timetk::tk_augment_fourier(optin_time, .periods=c(7,14,30,90,365), .K=2)

data_prep_fourier_tbl |> dplyr::slice_head(n=3) |> dplyr::glimpse()

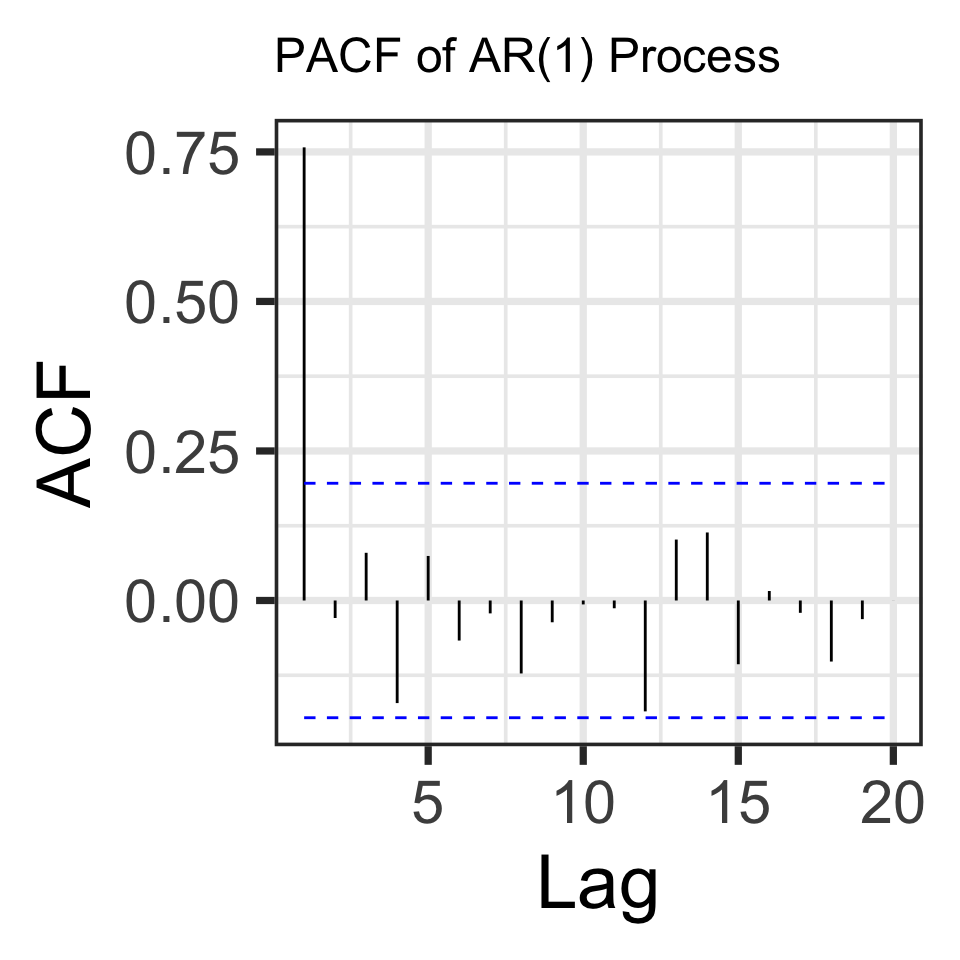
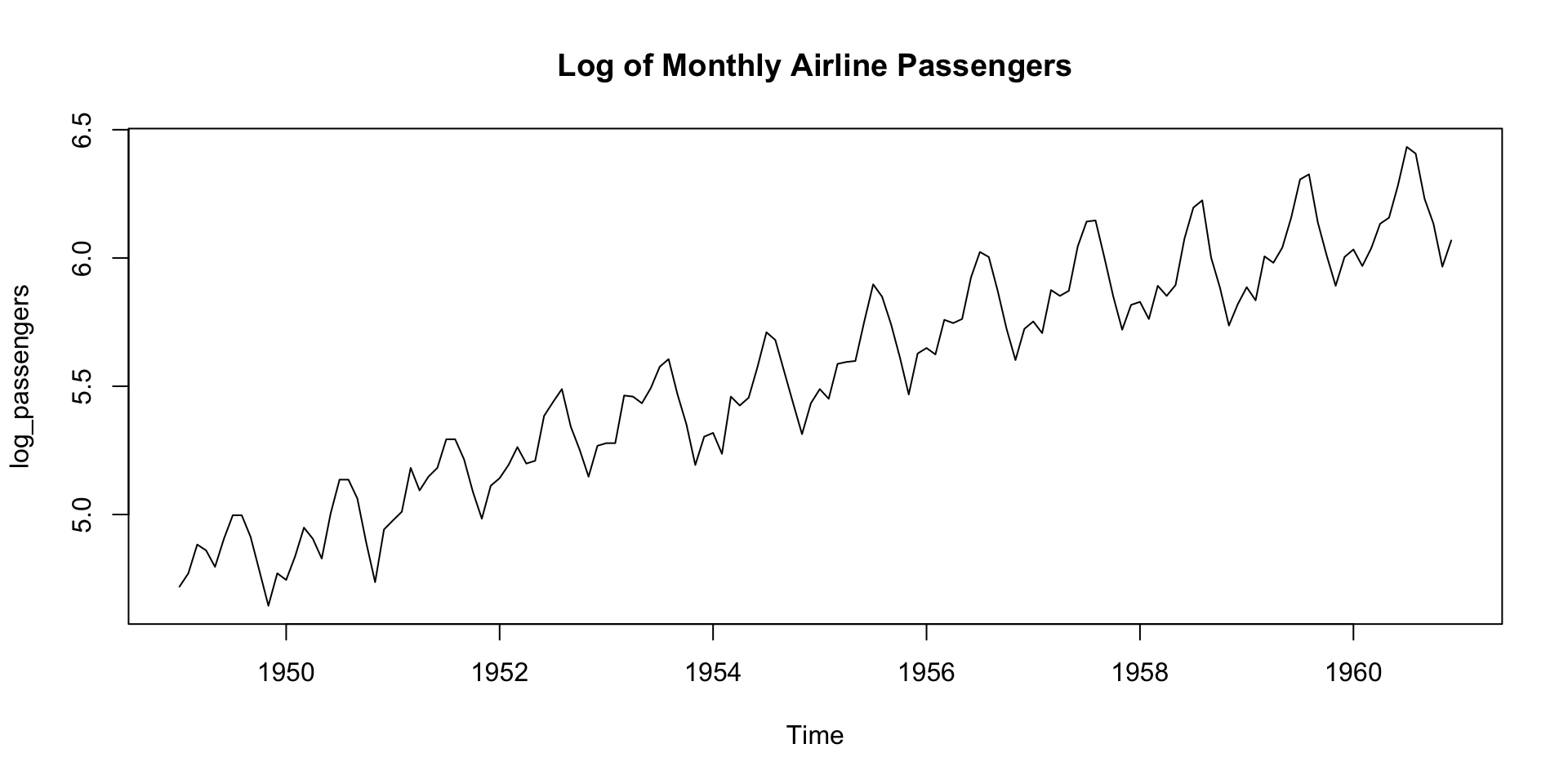
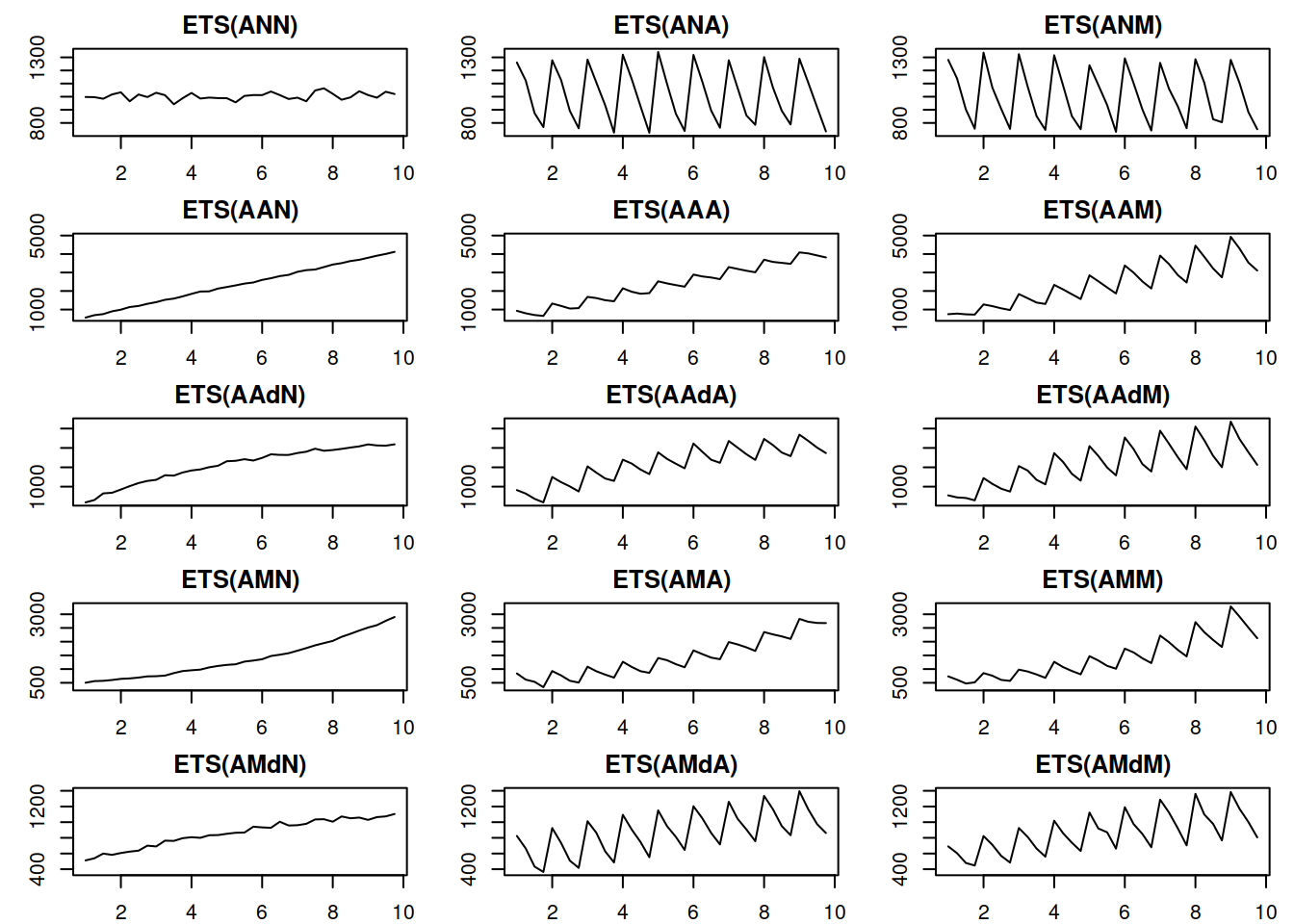
Rows: 3
Columns: 50
$ optin_time           <date> 2018-07-03, 2018-07-04, 2018-07-05
$ optins_trans         <dbl> -0.4919060, -0.1534053, -0.5779424
$ index.num            <dbl> 1530576000, 1530662400, 1530748800
$ diff                 <dbl> NA, 86400, 86400
$ year                 <int> 2018, 2018, 2018
$ year.iso             <int> 2018, 2018, 2018
$ half                 <int> 2, 2, 2
$ quarter              <int> 3, 3, 3
$ month                <int> 7, 7, 7
$ month.xts            <int> 6, 6, 6
$ month.lbl            <ord> July, July, July
$ day                  <int> 3, 4, 5
$ hour                 <int> 0, 0, 0
$ minute               <int> 0, 0, 0
$ second               <int> 0, 0, 0
$ hour12               <int> 0, 0, 0
$ am.pm                <int> 1, 1, 1
$ wday                 <int> 3, 4, 5
$ wday.xts             <int> 2, 3, 4
$ wday.lbl             <ord> Tuesday, Wednesday, Thursday
$ mday                 <int> 3, 4, 5
$ qday                 <int> 3, 4, 5
$ yday                 <int> 184, 185, 186
$ mweek                <int> 1, 1, 1
$ week                 <int> 27, 27, 27
$ week.iso             <int> 27, 27, 27
$ week2                <int> 1, 1, 1
$ week3                <int> 0, 0, 0
$ week4                <int> 3, 3, 3
$ mday7                <int> 1, 1, 1
$ optin_time_sin7_K1   <dbl> -9.749279e-01, -7.818315e-01, 2.256296e-13
$ optin_time_cos7_K1   <dbl> -0.2225209, 0.6234898, 1.0000000
$ optin_time_sin7_K2   <dbl> 4.338837e-01, -9.749279e-01, 4.512593e-13
$ optin_time_cos7_K2   <dbl> -0.9009689, -0.2225209, 1.0000000
$ optin_time_sin14_K1  <dbl> 7.818315e-01, 4.338837e-01, -1.128148e-13
$ optin_time_cos14_K1  <dbl> -0.6234898, -0.9009689, -1.0000000
$ optin_time_sin14_K2  <dbl> -9.749279e-01, -7.818315e-01, 2.256296e-13
$ optin_time_cos14_K2  <dbl> -0.2225209, 0.6234898, 1.0000000
$ optin_time_sin30_K1  <dbl> 1.126564e-13, -2.079117e-01, -4.067366e-01
$ optin_time_cos30_K1  <dbl> -1.0000000, -0.9781476, -0.9135455
$ optin_time_sin30_K2  <dbl> -2.253127e-13, 4.067366e-01, 7.431448e-01
$ optin_time_cos30_K2  <dbl> 1.0000000, 0.9135455, 0.6691306
$ optin_time_sin90_K1  <dbl> -0.8660254, -0.8290376, -0.7880108
$ optin_time_cos90_K1  <dbl> 0.5000000, 0.5591929, 0.6156615
$ optin_time_sin90_K2  <dbl> -0.8660254, -0.9271839, -0.9702957
$ optin_time_cos90_K2  <dbl> -0.5000000, -0.3746066, -0.2419219
$ optin_time_sin365_K1 <dbl> -0.2135209, -0.2303057, -0.2470222
$ optin_time_cos365_K1 <dbl> -0.9769385, -0.9731183, -0.9690098
$ optin_time_sin365_K2 <dbl> 0.4171936, 0.4482293, 0.4787338
$ optin_time_cos365_K2 <dbl> 0.9088176, 0.8939186, 0.8779601

Visualization

# Model
model_formula_fourier <- 
  as.formula(
    optins_trans ~ . +
      splines::ns(index.num
                  , knots=quantile(index.num, probs=c(0.25, 0.5, 0.75)))
  )

# Visualize
data_prep_fourier_tbl |> 
  timetk::filter_by_time(.start_date="2018-09-13") |> 
  timetk::plot_time_series_regression(
    .date_var = optin_time
    , .formula = model_formula_fourier
    , .show_summary = FALSE
    , .title = "Fourier + Cubic spline, 3 knots"
  )

Test-train splits

dat <- subscribers_tbl |> 
  timetk::summarize_by_time(optin_time, .by="day", optins=dplyr::n()) |> 
  timetk::pad_by_time(.pad_value=0) |> 
  timetk::filter_by_time(.start_date = "2018-12-15")

# Split Data 80/20
splits <- 
  timetk::time_series_split(
    data = dat
    , initial = "12 months"
    , assess = "1 months"
  )

splits |>
  timetk::tk_time_series_cv_plan() |>
  timetk::plot_time_series_cv_plan(.date_var = optin_time, .value = optins)

Feature engineering w/ recipes

time_rec <- dat |> 
  recipes::recipe(optins ~ ., data = rsample::training(splits)) |> 
  timetk::step_log_interval(optins, limit_lower = 0, offset = 1) |> 
  recipes::step_normalize(recipes::all_outcomes()) |> 
  timetk::step_timeseries_signature(optin_time) |> 
  timetk::step_fourier(optin_time, period = c(7,14,30,90,365), K=2)

time_rec |> recipes::prep(training = rsample::training(splits)) |> 
  recipes::bake(new_data = NULL) |> 
  timetk::plot_time_series_regression(
    .date_var = optin_time
    , .formula = optins ~ .
    , .show_summary = FALSE
  )

$optins
[1] 0

$optins
[1] 400

Workflows

# process engineering with workflows: ARIMA model
model_spec_arima <- modeltime::arima_reg() |>
    parsnip::set_engine("auto_arima")

recipe_spec_fourier <- 
  recipes::recipe(
    optins ~ optin_time
    , data = rsample::training(splits)
  ) |>
    timetk::step_fourier(optin_time, period = c(7, 14, 30, 90), K = 1) 

workflow_fit_arima <- workflows::workflow() |>
  workflows::add_recipe(recipe_spec_fourier) |>
  workflows::add_model(model_spec_arima) |>
  parsnip::fit(rsample::training(splits))

Workflows

# process engineering with workflows: linear model
model_spec_lm <- parsnip::linear_reg() |>
  parsnip::set_engine("lm") 

recipe_spec_linear <- 
  recipes::recipe(
    optins ~ optin_time
    , data = rsample::training(splits)
  ) |>
    timetk::step_fourier(optin_time, period = c(7, 14, 30, 90), K = 1) 

workflow_fit_linear <- workflows::workflow() |>
  workflows::add_recipe(recipe_spec_linear) |>
  workflows::add_model(model_spec_lm) |>
  parsnip::fit(rsample::training(splits))

Predict

models_tbl <- 
  modeltime::modeltime_table(workflow_fit_arima, workflow_fit_linear)

calibration_tbl <- models_tbl |>
  modeltime::modeltime_calibrate(new_data = rsample::testing(splits))

calibration_tbl |>
  modeltime::modeltime_forecast(
    new_data    = rsample::testing(splits),
    actual_data = dat
  ) |>
  modeltime::plot_modeltime_forecast(
    .legend_max_width = 25, # For mobile screens
    .interactive      = TRUE
  )

Evaluate

calibration_tbl |>
  modeltime::modeltime_accuracy() |>
  modeltime::table_modeltime_accuracy(
    .interactive = FALSE
  )

Accuracy Table
.model_id	.model_desc	.type	mae	mape	mase	smape	rmse	rsq
1	REGRESSION WITH ARIMA(2,0,1)(2,0,0)[7] ERRORS	Test	60.82	65.18	0.6	72.87	124.54	0.08
2	LM	Test	60.80	65.60	0.6	68.92	126.34	0.02

Re-fit

refit_tbl <- calibration_tbl |>
  # use all the data
  modeltime::modeltime_refit(data = dat)

refit_tbl |>
  modeltime::modeltime_forecast(h = "3 months", actual_data = dat) |>
  modeltime::plot_modeltime_forecast(
    .legend_max_width = 12, # For mobile screens
    .interactive      = TRUE
  )

Recap

• In this section we have worked with the tidymodels and timetk packages to build a workflow that facilitates building and evaluating multiple models.

• Combined with the recipes package we now have a complete data modeling framework for timeseries.